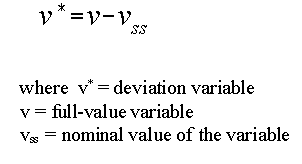
In control engineering we are usually interested in how things change around a particular steady-state called the nominal operating point. In solving the equations, we can use normal, full-valued, variables, but then the solution will be complicated by the steady-state information. This information is exactly the same at the start and end of the solution, but makes the algebra really messy. To get around this deviation variables are normally used. Deviation variables have a value which is equal to the full value variable minus the variables nominal, steady-state, value, i.e.
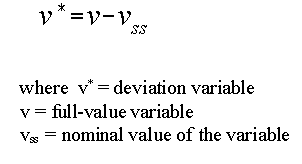
When you convert an equation to deviation variable form you have to convert all the variables to deviation variables. If you don't then you'll end up with stray steady-state information that will give the wrong solution (e.g. if 'y=x' was converted to 'y*=x' and x changed from 2 to 3, then the deviation in y, y* would be 3 (and y would become 5 (=y*+yss=3+2)). The correct value for y* is, of course, 1 and is equal to x*)
The long way to convert an equation to deviation variables is to write the steady-state version of the equation beneath it and subtract each term, e.g.
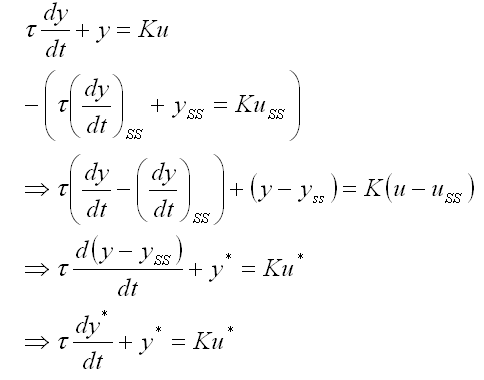
A quicker way to do the conversion is simply to do it by inspection - all you need to do is to write an asterisk against each time varying quantity in the equation. WARNING you need to be very careful when converting equations with non-linear quantities into deviation variable form. The correct way to do this is: identify the non-linear terms; put brackets around them; take the deviation of the whole term. As an example of what can go wrong if you don't do this consider the equation below when u changes from 4 to 9.
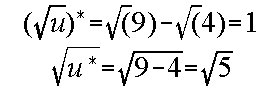
The correct answer is 1 !